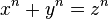Aujourd’hui, google nous propose un « doodle » (une image qui remplace le logo traditionnel sur leur page principale) qui contient une blague de matheux ! En effet, quand on survole l’image avec la souris, un texte obscur apparaît :

J’ai trouvé une merveilleuse démonstration de cette proposition mais ce doodle est trop étroit pour la contenir.

Le doodle en question. On peut y voir un énoncé simplifié du grand théorème de Fermat ainsi, entre autre, qu’un triangle rectangle.

Grand théorème de Fermat

Pierre de Fermat était un mathématicien du XVIIème à qui l’on doit en particulier deux théorèmes de théorie de nombres sobrement appelés « petit théorème de Fermat » et… « grand théorème de Fermat » [1]. On lui doit également des découvertes dans d’autres domaines, comme toujours avec les scientifiques de l’époque, notamment en optique.

En l’occurrence, c’est le grand théorème de Fermat qui nous intéresse ici. En effet, celui-ci stipule que :

Il n’existe pas de nombres entiers non nuls x, y et z tels que :

dès que n est un entier strictement supérieur à 2.

Tout est dit : Vous ne trouverez par exemple jamais deux entiers x et y tels que x^3 + y^3 = 42.

Et pour la blague ?

Dans l’ouvrage où il a exposé cette proposition, Fermat a écrit dans la marge :

J’ai trouvé une merveilleuse démonstration de cette proposition, mais la marge est trop étroite pour la contenir.

Fermat, Arithmetica de Diophante (traduction)

Or, la démonstration de ce théorème est en fait très récente : elle a été faite en 1994 par Andrew Wiles [2], un mathématicien grand breton. La subtilité de la blague réside dans le fait qu’en plus d’avoir nécessiter 350 ans, la démonstration en question fait plusieurs centaines de pages et fait appel à des concepts que l’on qualifiera pudiquement de « complexes ». En gros, soit Fermat avait une démonstration absolument géniale de simplicité sous le coude, soit il s’était trompé, soit il bluffait. Dans tous les cas, c’était quand même un effet d’annonce de compétition :

Hahaha ! Je connais la démo mais je vous laisse vous débrouiller ! Vous verrez, il y en a pour 5min (ou 350 ans, je sais plus lol).

Fermat (ou presque)

Et le triangle rectangle ?

Dans le théorème, il est précisé qu’il faut que n soit strictement supérieur à 2. En effet, dans le cas n=2, le théorème de Pythagore [3] correspond à un cas où cette équation a une solution. Par exemple, 3²+4²=5². D’où le triangle rectangle.

Comme quoi, les gens de chez Google ont de bonnes références !