Archives mensuelles : août 2011

Le bouton « j’aime », ce fléau

Posted on par
6

Je me rends compte avec effroi que, en dépit des promesses de mon premier post, je ne vous ai pas encore infligé d’article sur l’informatique. Or, il s’avère que nos amis d’outre-Rhin viennent de s’en prendre à Facebook, donnant lieu à des articles notamment dans Le Monde et Libération qui, s’ils ont le mérite d’exister et de mettre en évidence les problèmes liés à cet outil, n’entrent pas vraiment dans les détails. Ce qui ce conçoit tout à fait dans la mesure où ce n’est pas vraiment leur rôle. Notons d’ailleurs que les polices des pays nordiques demandent elles aussi des explications à la firme en question, notamment en ce qui concerne ce qu’il convient d’appeler « le bouton du délit». Sans plus attendre, regardons un peu ce qui coince.

Le problème du bouton « j’aime »

Je n’aime pas le bouton « j’aime » [1]. D’ailleurs, je ne suis pas le seul. Comme expliqué dans un article du site écrans.fr, le principal problème posé par ce bouton n’est pas d’ordre philosophique [2] mais bien technique : en effet, à partir du moment où un bouton j’aime est présent, facebook peut savoir un paquet de choses sans même que vous cliquiez. Nous étudierons le comment plus loin, regardons tout d’abord ce à quoi l’entreprise de M. Zuckerberg peut accéder. Vous me direz peut-être : « moi je m’en fous, je n’ai pas de compte chez toi donc tu ne risques pas de savoir grand chose ». Bien que vous ayez raison de ne pas me faire confiance [4], j’ai quand même accès à pas mal d’info : je sais que la personne qui a telle adresse IP aime ceci ou cela puisqu’elle fréquente ce site ou celui-la. Si cette adresse ne change pas, je peux accumuler pas mal d’info.

Les informations accessibles

Où que vous alliez sur internet, vous laissez des traces. Un paquet de traces, à moins de vous ingénier à ne pas le faire, mais ceci est une autre question. À titre d’exemple, j’utilise une extension de wordpress, statsurfer, pour connaître des statistiques diverses, comme le nombre de connexions sur ce blog. Or, sans faire quoi que ce soit de particulier, simplement en enregistrant les informations transitant normalement entre un site internet et votre ordinateur, ce plugin me permet de savoir :

  • Votre adresse IP.
  • Le pays duquel vous vous êtes connectés et même la ville (même si ce n’est pas très précis)
  • La page qui vous a mené à ce site et, du coup, le cas échéant les mots clefs que vous avez entrés dans votre moteur de recherche préféré et qui vous ont menés ici [3].
  • La ou les pages vues ici
  • Votre navigateur web (Firefox, Chrome, Opéra, Safari, Explorer (pas bien), Midori et j’en passe)
  • Votre système d’exploitation
  • L’heure de votre connexion ici

En ce qui me concerne, je peux vous assurer que ces données ne seront jamais divulguées et, si cela peut vous rassurer, que je ne m’intéresse qu’aux données dites « agrégées », c’est à dire pas à chaque visiteur mais à leur ensemble.

Capture d'écran de statsurfer

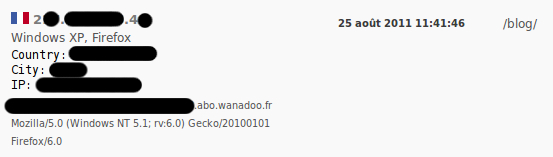
Un exemple d’entrée dans le tableau récapitulant qui est venu sur ce site. Alors que vous lisez, une autre s’est ajoutée vous correspondant. Dites vous bien que c’est pareil pour tous les sites — même si les logs apache sont moins jolis, certes).

Mettons que je sois facebook

Je vous propose maintenant une petite expérience de pensée. Imaginons un instant que je sois une célèbre entreprise américaine spécialisée dans le recueil d’informations personnelles des internautes. En usant d’artifices un tantinet fourbes, j’ai réussi à convaincre les administrateurs d’un nombre colossal de sites internet d’insérer un morceau de code à moi dans leur page. Celui-ci contient un bouton « Je suis actuellement connecté sur ce site et je souhaite le dire au monde entier » qui me permet de connaître plus finement les centres d’intérêts de mes usagers. Eh oui, puisqu’ils doivent être inscrits chez moi pour pouvoir l’utiliser, je sais exactement qui a cliqué dessus, quand, mais aussi quelle est son adresse IP, son pays, la page visitée précédemment, le navigateur web, etc. Surtout, en cliquant sur ce bouton, il a admis l’intérêt qu’il porte à ce contenu. C’est toujours ça d’information supplémentaire.

Qu’est-ce que je fais de cette masse de données ? Parce que vous croyez que je vais vous le dire ? Faites moi confiance, c’est pas comme si mon site était plein de failles de sécurité ou si je pratiquais une liberté d’expression à deux vitesses qui laisse tranquille les groupes ouvertement racistes mais ferme ceux qui déplaisent à de grandes enseignes du sous-vêtement.

Comment facebook collecte des infos

Comme dit précédemment, ce bouton permet à facebook de savoir qui est présent sur quel site, et ce sans même qu’il soit nécessaire d’avoir un compte. En effet, quand un site contient un tel bouton, il contient un réalité un code qui fait appel aux sites… facebook.net et fbcdn.net. Du coup, une requête [4] contenant toutes les infos précisées ci-dessus (navigateur, OS, IP, etc.) est envoyée aux serveurs de FB à chaque fois que vous connectez sur cette page, et ce même si vous n’y avez pas de compte.

Mais ce n’est pas tout : si vous y avez un compte et pour peu qu’un onglet facebook soit ouvert quelque part dans votre navigateur, ou bien si vous avez (à tort) choisi de rester connecté en permanence, un cookie est présent sur votre ordinateur. En gros, c’est un fichier qui est envoyé dans notre cas à facebook à chaque fois que vous vous y connectez et qui permet de vérifier votre identité. Jusque là tout va bien. Par contre, du coup, FB sait à quel site vous (car il sait qui vous êtes dans ce cas) vous connectez sans que vous ne cliquiez sur le bouton, et c’est bien là qu’est tout le problème.

La meilleure protection contre ce genre de pratique reste l’extension NoScript de Firefox. D’un usage un peu lourd au début, on s’y habitue très vite. De plus, les pubs sont également bloquées, ce qui est je trouve des plus agréables.

Cette partie peut être est un peu compliquée si l’on n’a aucune connaissance en réseau, n’hésitez pas à poser des questions dans les commentaires 😉

Conclusion

J’espère que les problèmes posés par ce bouton sont maintenant clairs et que vous vous accorderez par conséquents à penser que c’est effectivement un fléau. Le lecteur intéressé par les questions de vie privée pourra consulter avec profit [5] les ressources suivants :

  • Le site de la CNIL
  • Un article pratique du Monde
  • L’Express a une section entièrement dédiée à cette problématique. Les articles ne parlent pas de technique et sont donc très faciles d’accès.
[1] Blague pourrie indispensable : check.
[2] Encore qu’il y aurait probablement beaucoup de choses à dire sur cette habitude de demander aux utilisateurs de donner un avis binaire sur tout ce qu’ils voient sans que cela n’aie aucune incidence sur le contenu ainsi jugé, mais je m’égare.
[3] Ayons au passage une petite pensée pour ceux (russes apparemment) qui avaient cherché « lust » sur google, « luxure»  en anglais, et qui sont tombés sur ce site du fait de la mention qui est faite de l’exposition maintenant terminée « lust & last » au National Museet de Stockholm. Bwahaha.
[4] Quand on parle de réseaux informatiques, on appelle requête grosso modo une demande d’information envoyée à un serveur. Par exemple, quand vous avez tapez l’adresse de mon blog dans votre navigateur puis fait « entrer », une requête est partie en direction de mon serveur chez OVH, ce qui a provoqué le téléchargement de cette page pour qu’elle soit affichée par votre navigateur.
[5] Je suis paré pour la publication universitaire B)

HS : maintenant je comprends ce que ressentent les filles quand elles lisent des magazines féminins les prenant pour des demeurées puisqu’en faisant des recherches pour cet article, je suis tombé sur ça : un « article » à destination des « jeunes » qui consiste en une information et, surtout, en placement de produit… Et je ne parle pas du niveau de la langue et de l’étalage de clichés de rigueurs. C’est pas glorieux.

Google, ces p’tits rigolos

Posted on par
9

Aujourd’hui, google nous propose un « doodle » (une image qui remplace le logo traditionnel sur leur page principale) qui contient une blague de matheux ! En effet, quand on survole l’image avec la souris, un texte obscur apparaît :

J’ai trouvé une merveilleuse démonstration de cette proposition mais ce doodle est trop étroit pour la contenir.

le doodle google du crime

Le doodle en question. On peut y voir un énoncé simplifié du grand théorème de Fermat ainsi, entre autre, qu’un triangle rectangle.

Grand théorème de Fermat

Pierre de Fermat était un mathématicien du XVIIème à qui l’on doit en particulier deux théorèmes de théorie de nombres sobrement appelés « petit théorème de Fermat » et… « grand théorème de Fermat » [1]. On lui doit également des découvertes dans d’autres domaines, comme toujours avec les scientifiques de l’époque, notamment en optique.

En l’occurrence, c’est le grand théorème de Fermat qui nous intéresse ici. En effet, celui-ci stipule que :

Il n’existe pas de nombres entiers non nuls x, y et z tels que :
x^n + y^n = z^n
dès que n est un entier strictement supérieur à 2.

Tout est dit : Vous ne trouverez par exemple jamais deux entiers x et y tels que x^3 + y^3 = 42.

Et pour la blague ?

Dans l’ouvrage où il a exposé cette proposition, Fermat a écrit dans la marge :

J’ai trouvé une merveilleuse démonstration de cette proposition, mais la marge est trop étroite pour la contenir.

Fermat, Arithmetica de Diophante (traduction)

Or, la démonstration de ce théorème est en fait très récente : elle a été faite en 1994 par Andrew Wiles [2], un mathématicien grand breton. La subtilité de la blague réside dans le fait qu’en plus d’avoir nécessiter 350 ans, la démonstration en question fait plusieurs centaines de pages et fait appel à des concepts que l’on qualifiera pudiquement de « complexes ». En gros, soit Fermat avait une démonstration absolument géniale de simplicité sous le coude, soit il s’était trompé, soit il bluffait. Dans tous les cas, c’était quand même un effet d’annonce de compétition :

Hahaha ! Je connais la démo mais je vous laisse vous débrouiller ! Vous verrez, il y en a pour 5min (ou 350 ans, je sais plus lol).

Fermat (ou presque)

Et le triangle rectangle ?

Dans le théorème, il est précisé qu’il faut que n soit strictement supérieur à 2. En effet, dans le cas n=2, le théorème de Pythagore [3] correspond à un cas où cette équation a une solution. Par exemple, 3²+4²=5². D’où le triangle rectangle.

Comme quoi, les gens de chez Google ont de bonnes références !

[1] Parce que des fois on a pas envie de se fouler.
[2] Du coup, on devrait parler du théorème de Miles et non du grand théorème de Fermat puisque ce sont en théorie ceux qui démontrent un théorème qui lui donnent leur nom. Que voulez-vous, l’habitude est puissante, mais chez les mathématiciens !
[3] Le théorème de Pythagore nous dit que, dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des côtés opposés. Par exemple, si un triangle rectangle a deux côtés de 3cm et 4cm qui forment un angle droit, alors le dernier (l’hypothénuse) fera 5cm car 3²+4² = 9+16 = 25 = 5².

15 août

Posted on par
2

Un 15 août à Stockholm. Il fait 18°C. Le vent souffle et s’accompagne parfois d’un peu de pluie. Le soleil semble se coucher à 21h, mais l’obscurité induite par l’épaisse couverture nuageuse fausse probablement ce résultat. Le steak haché local n’a manifestement pas compris le sens du mot « goût».

Et en plus ce n’est pas jour férié.

Je suis sûr que vous êtes tous super jaloux !

De toute façon j’m’en fous, j’ai des gâteaux trop cool pour me tenir chaud 😀

Mais pourquoi π² / 6 ?

Posted on par
9

Les Suédois étant toujours aussi peu nombreux sur le campus (contrairement aux Allemands, aux Espagnols et surtout aux Français), j’ai beaucoup de mal à réunir suffisamment de matière pour rédiger un article sur le Suédois, le gus. Ce n’est pourtant pas faute d’essayer, mais bref. Comme suggéré dans les commentaires par un historien perplexe devant le nom du présent site, je m’en vais de ce pas lancer la rubriques « les maths, c’est magique ! » de ce blog en répondant à la question qui a donné son titre à cet article : mais pourquoi π² / 6 ?

Déjà, π, c’est cool

Je ne vous ferai pas l’offense de prétendre vous apprendre que π désigne le rapport de la circonférence du cercle à son diamètre. Jusque-là, je pense que tout va bien. Mais ce nombre a plusieurs caractéristiques intéressantes.

π est irrationnel

Cela ne veut bien évidemment pas dire que π fait des mathématiques financières ou raconte à qui veut l’entendre que la fin du monde est pour décembre 2012. En maths, on appelle nombre irrationnel un nombre qui ne peut pas s’écrire sous forme de fraction. Par exemple, 3/7 est rationnel, tout comme 12 (qui s’écrit 12/1) ou encore 0,11111.. avec « une infinité de 1 »[1] qui s’écrit 1/9. π ne peut pas s’écrire sous forme de fraction, cela a été démontré au XVIIIème par Jean-Henri Lambert. On peut néanmoins s’en approcher autant qu’on veut pour peu que l’on ait à disposition une puissance de calcul suffisante. En effet, π est la limite de plusieurs série, c’est à dire qu’en ajoutant une « infinité »[1] de termes bien précis, on obtiendrait ce nombre. Même s’il est impossible de faire une telle somme, on peut l’approcher suffisamment en ajoutant un « grand nombre »[2] de ces termes. C’est notamment en ayant recours à de telles séries que l’on peut appliquer la formule de Machin[3] pour calculer autant de décimales que la puissance de calcul utilisée le permet.>

π est transcendant

Point de jugement de valeur ici, simplement une autre caractéristique mathématique. π n’est la racine d’aucun polynôme à coefficient entiers. « Fort bien» , me direz-vous, « mais cela ne me dit ni ce qu’est une racine ni ce qu’est un polynôme ». Remédions à cela.

Bonhomme New Age tout bleu

Le rapport entre la transcendance divine et la transcendance mathématique ? C’est facile : il n’y en a aucun ! Notre ami bleuté l’aurait su s’il n’avait pas abusé de substances illicites néfastes (et lu cet article).

  • Polynôme : on appelle polynôme une fonction[4] de la forme P(X) = a0 + (a1 × X) + (a2 × X²) + (a3 × X^3) + … + (aN × X^N) où a0, a1, a2, a3… et aN sont des nombres. Par exemple, Q(X) = 3,5 + 2×X + π×X² est un polynôme.
  • Racine : Une racine d’un polynôme est un nombre qui l’annule. C’est à dire que si P est un polynôme et r une de ses racines, alors P(r) = 0. Par exemple, 2 est une racine de P(X) = 2 - 3×X + X². En effet, P(2) = 2-3×2+2² = 2-6+4 = 0.

Par exemple, la racine de 2 n’est pas transcendante puisqu’elle est racine de P(X) = 1×X²-2 et que 1 et 2 sont entiers.

Une fois ceci précisé, il devrait être clair que comme π est transcendant, on ne trouvera jamais de polynômes P à coefficients entiers (c’est à dire pour lesquels les nombres a0,…,aN sont entiers) tels que P(π) = 0.

On pourrait disserter sur π pendant des pages, d’ailleurs, wikipedia ne s’en prive pas. Mais intéressons-nous maintenant de plus près à « π² / 6 ».

Ensuite, π² / 6, ça l’est encore plus

Somme des 1/n²

J’ai parlé plus haut de série. Et bien π² / 6 est la limite vers laquelle converge une série : celle dite « des 1/n² ». En fait, si on additionne 1 (1/1²), 1/4 (1/2²), 1/9 (1/3²), 1/16 (1/4²),… On s’approche de plus en plus de π² / 6. Si tant est que cela ait un sens, on tomberait sur π² / 6 en ajoutant une infinité de ces termes[1]. Ce résultat, surnommé « problème de Bâle » a été trouvé par Euler, un de ces mathématiciens dont on trouve le nom partout puisqu’il a travaillé dans énormément de domaines, y compris en physique. Il doit se partager avec Gauss la moitié des noms de théorèmes de mathématiques et de physique ![5]

Euler, par Emanuel Handmann

Euler, par Emanuel Handmann. Aurai-je moi aussi un beau chapeau quand j’aurai fini mes études ? Mystère…

La fonction zêta de Riemann

Les mathématiques sont loin d’être « terminées », il reste en effet beaucoup de problèmes non résolu à l’heure actuelle. L’un d’entre eux est le problème des « pôles de la fonction ζ de Riemann ». « Pôle » a ici un sens similaire à celui de racine dans le cas des polynôme : c’est un point en lequel la fonction s’annule. On pense à l’heure actuelle savoir grosso modo où ils se trouvent, mais cela n’a pas été démontré. D’ailleurs, si vous arrivez à le démontrer (ou à démontrer que ce qu’on croit est faux), vous êtes riche puisqu’il s’agit d’un des problèmes du millénaire. Résolvez-le et vous gagnerez un million de dollars ! Le rapport avec π² / 6 ?

ζ(2) = π² / 6

Et je veux ce million.

Conclusion

J’espère avoir été clair, n’hésitez pas à poser des questions dans les commentaires si des points sont obscures. J’espère aussi avoir montré pourquoi π² / 6 est un nom parfait pour ce site ! Demain, j’ai rendez-vous avec le responsable des mathématiques à KTH pour affiner mes choix d’options, je devrais donc bientôt savoir à quelle sauce je vais être mangé. Enfin !

[1] La notion « d’infini » est beaucoup plus compliquée qu’il n’y paraît et fait appel à celle de limite qui est également loin d’être triviale. Considérez ces contenus entre guillemets comme des simplifications pédagogiques 😉

[2] De plus, il existe des méthodes mathématiques permettant de connaître à l’avance une majoration de l’erreur en fonction du nombre de termes ajoutés. Cela signifie qu’avant même de lancer le calcul et sans connaître la « vraie » valeur de π, on peut savoir que notre calcul nous donnera par exemple les 10 premières décimales justes, la suite étant a priori (et de fait, sauf chance incroyable) fausse.

[3] Du nom de M. Machin. Oui oui, ce n’est pas un trou de mémoire de ma part, il s’appelait vraiment Machin !

[4] Les fonctions seront peut-être l’objet d’un article dans le futur. N’ayant aucune idée quant à l’éventuelle date de publication de celui-ci, vous pouvez consulter en attendant consulter la page de wikipedia.

[5] Wikipedia liste les théorèmes de Gauss mais n’a pas de page dédiée pour Euler. Ils n’en sont pas moins nombreux, croyez-moi !

Le Suédois : la Langue

Posted on par
8

Lors donc, puisque je vis actuellement sur ses terres, je m’en vais vous décrire du mieux que je peux le Suédois, qu’il s’agisse du Suédois en tant que langue ou bien de l’habitant de la Suède. Tout d’abord, intéressons-nous de plus près à ce dialecte barbare.

Considération générales

On m’avait dit avant de partir que le Suédois ressemblait beaucoup à de l’Allemand mâtiné de sonorité Japonaise, ce qui m’a beaucoup enchanté dans le mesure où je n’ai absolument aucune notion dans aucune de ces deux langues. Apparemment, c’est le cas (du moins si j’en crois certains de mes camarades KTH-iens).

La grammaire est assez étrange : il n’y a pratiquement pas de conjugaison. Ainsi, « j’étudie » devient « jag studerar » et « nous étudions » se transforme en « vi studerar ». Tout pareil. Il y a par contre plein de verbes irréguliers au passé mais ça reste gérable. Notez au passage le « vi » pour « nous » qui ressemble étrangement au « we » anglais. Il y a six personnes, comme en français : je, tu, [il/elle/le truc en « en »/le truc en « ett »], nous, vous, ils. Comme en Anglais, on utilise un terme différent pour les objets que pour les humains.

Enfin, vous le savez probablement déjà mais l’alphabet Suédois compte plus de lettres, vingt-neuf pour être précis. À l’alphabet français il faut ajouter : ‘å'[1] (qui se comporte comme un ‘o’), ‘ö’ et ‘ä’.

Ett-ord och en-ord

Les ett-mots et les en-mots

En Suédois, il y a deux types de types de mots utilisant deux types d’articles indéfinis singuliers : ceux pour lesquels il s’agit de « ett » et ceux pour lesquels c’est « en ». Ces différences se répercutent dans d’autres situations. Ainsi, le pronom pour « le truc en en » est « den » alors que celui pour « le truc en ett » est « det ». Le mot « Quoi/Quelle » (équivalent de l’anglais « what ») change aussi : « vilken, vilket » et, au pluriel, « vilka ».

Structure

La syntaxe des phrases obéit à une structure assez rigide et très particulière ; chaque mot à sa place dans la phrase et n’allez pas vous aviser de la changer. Dans le cas contraire, les grammars nazis locaux vous jetteront des cailloux et, plus gênant, les autochtones risquent de ne pas vous comprendre.

Les vikings aussi avaient des problèmes

Beaucoup de vikings se sont entretués à cause de différences quant à la façon de prononcer un même mot. Source ? Et puis quoi encore…

Prononciation

La principale difficulté du Suédois ne vient pas tant de sa grammaire, relativement simple, que de sa prononciation. En effet, si la compréhension écrite ne pose pas problème, l’oral est… comment dire… d’une intelligibilité plus aléatoire[2]. L’écriture ne fournit qu’une vague indication en ce qui concerne la façon dont la phrase doit être prononcée. Tout d’abord, comme en Français, la prononciation de certaines lettres dépend de la suivante. Par exemple, ‘g’ peut se prononcer « gue » ou « ye » (du moins en théorie). Ensuite, l’accent tonique, très important, n’est pas noté. Enfin, et plus embêtant, l’usage impose de prononcer certains mots d’une façon qui n’a rien à voir avec son écriture. Ou alors seulement vaguement. Ainsi, vingt-deux s’écrit « tjugotvå » mais se prononce « chutvo » : la syllabe « go » passe complètement à la trappe ! De la même façon, dans certaines situations, le pronom « du » (tu en Français) se prononce… « ru ». Pourquoi ? Parce que.

Conclusion

J’espère avoir vous donné un aperçu fidèle de la langue suédoise avec cet article. Si vous avez des questions sur cette langue merveilleuse, n’hésitez pas à mes les poser dans les commentaires, je répondrai du mieux que je peux !

Je vais à 17h « visiter » un cours de Français (cf. article précédent), ça devrait alimenter la suite : « le Suédois, le Gus (et la Guse) » !

[1] Pour les linuxiens, le code unicode de cette lettre étant « e5 », vous pouvez faire Ctrl+Maj+u puis, quand un ‘u’ souligné apparaît, taper « e5 ». Un å devrait apparaître. Les windowsiens, revenez quand votre OS supportera UTf-8 en natif 😛

[2] Je ne pensais pas arriver à la placer celle-là ! 

C’est la rentrée !

Posted on par
8

… Enfin, pour moi en tout cas. En effet, mes cours de Suédois ont déjà commencé, je suis donc en mesure de me présenter et de baragouiner deux-trois trucs. Par exemple, bonjour/salut se dit « Hej ! » (prononcez « Hé » ou « Hay ») et au revoir/salut… « Hej Hej ! ». Jusque là ça va.

Déjà une star !

À peine sorti de mon premier cours de Suédois, je me suis fait interviewé par SVT1, la première chaîne de Suède. La journaliste l’a décrite comme la « BBC de Suède ». Elle voulait avoir mon point de vue éclairé (de personne qui n’y connaît rien et débarque dans un pays sans en parler la langue) sur le fait que KTH fasse maintenant payer les étrangers venant de pays ne faisant pas partie de l’UE.

À moi la célébrité, mwahahahaha \o/

Un cerbere Art-Déco

Deux cerbères de pierre gardent l’entrée de KTH.

KTH

En Suédois, KTH se prononce « Ko Té Ho », avec des « o » comme dans « pot » et un « h » aspiré. Mais laissez-moi vous parler de cette école exceptionnelle. Comme vous pouvez en juger par les multiples photos parsemant cet article, KTH, c’est classe. C’est même LA classe. Je vous accorde qu’il faut aimer la brique rouge et l’art déco, mais on ne peut en tout cas nier que les bâtiments ont un certain cachet. En tout cas bien plus que certaines écoles françaises de ma connaissance… De plus, contrairement à ces mêmes écoles, KTH se trouve vraiment à Stockholm, et non dans quelque obscure banlieue située à 30min du centre-ville. Les mauvaises langues auront tôt fait de remarquer que « c’est bien la peine d’avoir des locaux à deux pas du centre-ville si c’est pour envoyer ses étudiants vivre à 45min de ceux-ci dans une non moins obscure banlieue ». Elles n’auront pas tort.

La cour intérieure

Une première vue de l’intérieur de la cour principale de KTH.

Les KTH-iens

Au-delà des locaux, intéressons-nous un peu à ceux qui les peuplent. Pour l’instant, il ne s’agit pratiquement que d’étudiants ERASMUS, dont une armée de français (on ne constitue peut-être pas la moitié des effectifs, mais on ne doit pas en être loin), plein d’allemands, de chinois et d’espagnols. D’autres nationalités sont plus ponctuellement présentes, notamment : autrichienne, sud coréenne, japonaise, turque, suisse, estonienne, hollandaise, singapourienne, ukrainienne et vénézuelienne (et je ne parle que de gens que j’ai rencontré, au moins de loin). L’auberge espagnole, c’était un truc de chochotte.

Re: La cour intérieure

Une deuxième vue de l’intérieur de la cour principale de KTH.

Point intéressant : un jeune homme de l’association étudiante chargée de l’accueil des étrangers (i.e : moi et mes comparses) nous a décrit sommairement les suédois afin que l’on sache un peu à quoi nous attendre. Apparemment, il y a une règle implicite par ici : « on ne parle pas aux gens ». Ça risque de ne pas être pratique. Il a également fait l’apologie de ce comic qui décrit, selon lui toujours, fidèlement la façon dont les scandinaves se voient entre eux. En gros, le Suédois typique serait un genre de schtroumpf à lunettes fan d’informatique. Ç’aurait pu être bien pire.

Pour remédier à la quasi-absence d’autochtones dans ma vie de tous les jours, j’ai répondu à une invitation du professeur de Français de KTH pour « visiter » un de ses cours (c’est le terme employé). Hum.

Lui : Et vous voyiez, là, c’est les tables. Devant, il y a des chaises sur lesquelles on met les étudiants pour qu’ils bossent.
Moi : Ooooooh ! Et même qu’ils sont dirigés vers le prof’ pour pouvoir écouter ce qu’il dit ! Dingue !
Lui : Et oui, on est très pragmatiques en Suède.
Moi : Et donc ça je suppose que c’est un tableau noir ?
Lui : C’est cela même.
Moi : Pas croyab’ !

Et en France on est très drôle. Surtout moi.

Désolé.

Forward: Re: La cour intérieure

Une troisième vue de l’intérieur de la cour principale de KTH. C’est la dernière (de cet article), promis !

Paperasse mon amie

Que serait une inscription sans la paperasse de circonstance ? Pratique ? Cool ? Agréable ? Certes, mais également assez peu réaliste, hélas. Je suis en ce moment en plein dedans, aussi je n’écrirai pas plus longtemps. Je dois notamment faire un « educated guess » (i.e : « deviner intelligemment » dans la langue de Molière) quant au choix de mes cours. Heureusement que les Suédois sont sensés être des nazis de l’organisation. Enfin, terminons sur un point positif : ça commence à cailler \o/